Interval (mathematics)
In mathematics, a (real) interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers 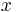 satisfying
satisfying 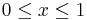 is an interval which contains
is an interval which contains 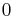 and
and 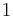 , as well as all numbers between them. Other examples of intervals are the set of all real numbers
, as well as all numbers between them. Other examples of intervals are the set of all real numbers  , the set of all negative real numbers, and the empty set.
, the set of all negative real numbers, and the empty set.
In fact, intervals are meaningful in any (totally or partially) ordered set, not just in the reals; so one can have intervals of rational numbers, integers, computer-representable floating point numbers, or subsets of a set (ordered by inclusion), for example.
Real intervals play an important role in the theory of integration, because they are the simplest sets whose "size" or "measure" or "length" is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure.
Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Contents |
Notations for intervals
The interval of numbers between 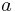 and
and  , including
, including 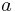 and
and  , is often denoted
, is often denoted ![[a,b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2c3d331bc98b44e71cb2aae9edadca7e.png) . The two numbers are called the endpoints of the interval.
. The two numbers are called the endpoints of the interval.
Excluding the endpoints
To indicate that one of the endpoints is to be excluded from the set, many writers substitute a parenthesis for the corresponding square bracket. Thus, in set builder notation,
Note that 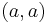 ,
, 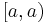 , and
, and ![(a,a]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/743d353831da0479f6e8920d0e0fbf80.png) denote the empty set, whereas
denote the empty set, whereas ![[a,a]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/dd54872a17a88b90afd2d0dd4292be27.png) denotes the set
denotes the set  . When
. When 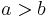 , all four notations are usually assumed to represent the empty set.
, all four notations are usually assumed to represent the empty set.
The ISO notation
International standard ISO 31-11 also defines another notation for intervals, which seems to be more commonly taught in Europe and South America. It uses an inwards pointing bracket to indicate inclusion of the endpoint, and outwards-pointing bracket for exclusion:
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation 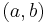 is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. The notation
is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. The notation ![[a,b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2c3d331bc98b44e71cb2aae9edadca7e.png) too is occasionally used for ordered pairs, especially in computer science.
too is occasionally used for ordered pairs, especially in computer science.
Some authors use ![]a,b[](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e46b2a760c57eb995b62bd166b835b1e.png) to denote the complement of the interval
to denote the complement of the interval 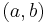 ; namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
; namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
In countries where numbers are written with a decimal comma, a semicolon may be used as a separator, to avoid ambiguity.
Infinite endpoints
In both styles of notation, one may use an infinite endpoint to indicate that there is no bound in that direction. Specifically, one may use  or
or  (or both). For example,
(or both). For example, 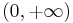 is the set of all positive real numbers, and
is the set of all positive real numbers, and 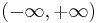 is the set of real numbers.
is the set of real numbers.
The notations ![[-\infty,b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d7ada7235c473c7b1a44b0b92fc9040d.png) ,
, 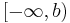 ,
, ![[a,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/77c803ddf2aed92a1321c3aa75ff5567.png) , and
, and ![(a,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/40977d617dd7f71819816eadf7d2101d.png) are ambiguous. For authors who define intervals as subsets of the real numbers, those notations are either meaningless, or equivalent to the open variants. In the latter case, the interval comprising all real numbers is both open and closed,
are ambiguous. For authors who define intervals as subsets of the real numbers, those notations are either meaningless, or equivalent to the open variants. In the latter case, the interval comprising all real numbers is both open and closed, ![(-\infty,+\infty) = [-\infty,+\infty] = [-\infty,+\infty) = (-\infty,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6be5b64a2d7bd3fb0fa0b6a1fc7687c0.png) .
.
Integer intervals
When 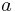 and
and  are integers, the notation
are integers, the notation ![[a\;..\;b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/417bf267464460771330ec8cfc4d5957.png) ,
, 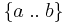 , or just
, or just  is sometimes used to indicate the interval of all integers between
is sometimes used to indicate the interval of all integers between 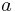 and
and  , including both. This notation is used in some programming languages; in Pascal, for example, it is used to define the set of valid indices of a vector.
, including both. This notation is used in some programming languages; in Pascal, for example, it is used to define the set of valid indices of a vector.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing 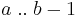 ,
, 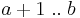 , or
, or  . Alternate-bracket notations like
. Alternate-bracket notations like 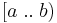 or
or 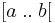 are rarely used for integer intervals.
are rarely used for integer intervals.
Terminology
An open interval does not include its endpoints, and is indicated with parentheses. For example 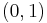 means greater than 0 and less than 1. Conversely, a closed interval includes its endpoints, and is denoted with square brackets. For example
means greater than 0 and less than 1. Conversely, a closed interval includes its endpoints, and is denoted with square brackets. For example ![[0,1]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ccfcd347d0bf65dc77afe01a3306a96b.png) means greater than or equal to 0 and less than or equal to 1.
means greater than or equal to 0 and less than or equal to 1.
A degenerate interval is any set consisting of a single real number. Some authors include the empty set in this definitions. An interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, or size of the interval. The size of unbounded intervals is usually defined as  , and the size of the empty interval may be defined as 0 or left undefined.
, and the size of the empty interval may be defined as 0 or left undefined.
The centre of bounded interval with endpoints 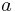 and
and  is
is 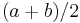 , and its radius is the half-length
, and its radius is the half-length 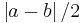 . These concepts are undefined for empty or unbounded intervals.
. These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it has no minimum (an element that is smaller than all other elements); right-open if it has no maximum; and open if it has both properties. The interval 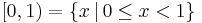 , for example, is left-closed and right-open. The empty set and the set of all reals are open intervals, while the set of non-negative reals, for example, is a right-open but not left-open interval. The open intervals coincide with the open sets of the real line in its standard topology.
, for example, is left-closed and right-open. The empty set and the set of all reals are open intervals, while the set of non-negative reals, for example, is a right-open but not left-open interval. The open intervals coincide with the open sets of the real line in its standard topology.
An interval is said to be left-closed if it has a minimum element, right-closed if it has a maximum, and simply closed if it has both. These definitions are usually extended to include the empty set and to the (left- or right-) unbounded intervals, so that the closed intervals coincide with closed sets in that topology.
The interior of an interval 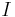 is the largest open interval that is contained in
is the largest open interval that is contained in 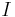 ; it is also the set of points in
; it is also the set of points in 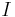 which are not endpoints of
which are not endpoints of 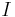 . The closure of
. The closure of 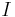 is the smallest closed interval that contains
is the smallest closed interval that contains 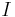 ; which is also the set
; which is also the set 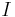 augmented with its finite endpoints.
augmented with its finite endpoints.
For any set  of real numbers, the interval enclosure or interval span of
of real numbers, the interval enclosure or interval span of  is the unique interval that contains
is the unique interval that contains  and does not properly contain any other interval that also contains
and does not properly contain any other interval that also contains  .
.
Classification of intervals
The intervals of real rumbers can be classified into eleven different types, listed below; where 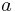 and
and  are real numbers, with
are real numbers, with 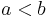 :
:
- empty:
![[b,a] = (a,a) = [a,a) = (a,a] = \{ \} = \emptyset](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/55ab796eb298fb4b1565631b0ceab5ce.png)
- degenerate:
![[a,a] = \{a\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/23e5436dac61e81c98084fc9874a93f5.png)
- proper and bounded:
- open:
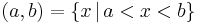
- closed:
![[a,b]=\{x\,|\,a\leq x\leq b\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5115289a339dec022f353a4f084f6bd4.png)
- left-closed, right-open:

- left-open, right-closed:
![(a,b]=\{x\,|\,a<x\leq b\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/35d71568e9dfcc7690c0481f698a6bd2.png)
- open:
- left-bounded and right-unbounded:
- left-open:
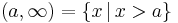
- left-closed:
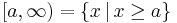
- left-open:
- left-unbounded and right-bounded:
- right-open:
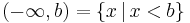
- right-closed:
![(-\infty,b]=\{x\,|\,x\leq b\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/325ca53d73f7db8d7a7591e8fe05f037.png)
- right-open:
- unbounded at both ends:
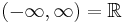
Intervals of the extended real line
In some contexts, an interval may be defined as a subset of the extended real numbers, the set of all real numbers augmented with 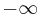 and
and  .
.
In this interpretation, the notations ![[-\infty,b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d7ada7235c473c7b1a44b0b92fc9040d.png) ,
, 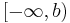 ,
, ![[a,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/77c803ddf2aed92a1321c3aa75ff5567.png) , and
, and ![(a,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/40977d617dd7f71819816eadf7d2101d.png) are all meaningful and distinct. In particular,
are all meaningful and distinct. In particular, 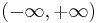 denotes the set of all ordinary real numbers, while
denotes the set of all ordinary real numbers, while ![[-\infty,+\infty]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/936cbe1fb6394ff85b26a5e76e81fcd5.png) denotes the extended reals.
denotes the extended reals.
This choice affects some of the above definitions and terminology. For instance, the interval 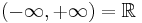 is closed in the realm of ordinary reals, but not in the realm of the extended reals.
is closed in the realm of ordinary reals, but not in the realm of the extended reals.
Properties of intervals
The intervals are precisely the connected subsets of  . It follows that the image of an interval by any continuous function is also an interval. This is one formulation of the intermediate value theorem.
. It follows that the image of an interval by any continuous function is also an interval. This is one formulation of the intermediate value theorem.
The intervals are also the convex subsets of  . The interval enclosure of a subset
. The interval enclosure of a subset 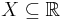 is also the convex hull of
is also the convex hull of  .
.
The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other (e.g., ![(a,b) \cup [b,c] = (a,c]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b73c4ef824664170bcb8813a6b80fe80.png) ).
).
If  is viewed as a metric space, its open balls are the open bounded sets
is viewed as a metric space, its open balls are the open bounded sets 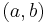 , and its closed balls are the closed bounded sets
, and its closed balls are the closed bounded sets ![[a,b]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
Any element 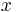 of an interval
of an interval 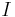 defines a partition of
defines a partition of 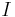 into three disjoint intervals
into three disjoint intervals  : respectively, the elements of
: respectively, the elements of 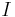 that are less than
that are less than 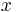 , the singleton
, the singleton ![[x,x] = \{x\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4e71ac1de83aa6f117ef1023e562eaaf.png) , and the elements that are greater than
, and the elements that are greater than 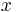 . The parts
. The parts 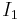 and
and 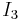 are both non-empty (and have non-empty interiors) if and only if
are both non-empty (and have non-empty interiors) if and only if 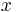 is in the interior of
is in the interior of 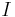 . This is an interval version of the trichotomy principle.
. This is an interval version of the trichotomy principle.
Dyadic intervals
A dyadic interval is a bounded real interval whose endpoints are 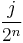 and
and 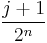 , where
, where  and
and 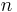 are integers. Depending on the context, either endpoint may or may not be included in the interval.
are integers. Depending on the context, either endpoint may or may not be included in the interval.
Dyadic intervals have some nice properties, such as the following:
- The length of a dyadic interval is always an integer power of two.
- Every dyadic interval is contained in exactly one "parent" dyadic interval of twice the length.
- Every dyadic interval is spanned by two "child" dyadic intervals of half the length.
- If two dyadic intervals overlap, then one of them must be a subset of the other.
The dyadic intervals thus have a structure very similar to an infinite binary tree.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinement, multigrid methods, and wavelet analysis.
Multi-dimensional intervals
In many contexts, an 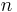 -dimensional interval is defined as a subset of
-dimensional interval is defined as a subset of 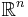 that is the Cartesian product of
that is the Cartesian product of 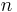 intervals,
intervals, 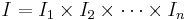 , one on each coordinate axis.
, one on each coordinate axis.
For 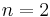 , this generally defines a rectangle whose sides are parallel to the coordinate axes; for
, this generally defines a rectangle whose sides are parallel to the coordinate axes; for 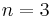 , it defines an axis-aligned rectangular box.
, it defines an axis-aligned rectangular box.
A facet of such an interval 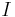 is the result of replacing any non-degenerate interval factor
is the result of replacing any non-degenerate interval factor  by a degenerate interval consisting of a finite endpoint of
by a degenerate interval consisting of a finite endpoint of  . The faces of
. The faces of 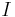 comprise
comprise 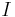 itself and all faces of its facets. The corners of
itself and all faces of its facets. The corners of 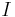 are the faces that consist of a single point of
are the faces that consist of a single point of 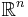 .
.
Complex intervals
Intervals of complex numbers can be defined as regions of the complex plane, either rectangular or circular.[1]
See also
- Inequality
- Interval graph
- Interval arithmetic
- Interval finite element
References
- ↑ Complex interval arithmetic and its applications, Miodrag Petković, Ljiljana Petković, Wiley-VCH, 1998, ISBN 9783527401345
External links
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval Notation Basics
- Interval computations website
- Interval computations research centers
- Interval Notation by George Beck, Wolfram Demonstrations Project.
- Weisstein, Eric W., "Interval" from MathWorld.
![\begin{align}
(a,b) &= \{x\in\R\,|\,a<x<b\}, \\{}
[a,b) &= \{x\in\R\,|\,a\le x<b\}, \\
(a,b] &= \{x\in\R\,|\,a<x\le b\}, \\{}
[a,b] &= \{x\in\R\,|\,a\le x\le b\}.
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2c0ed6b11710aceeae881a846468832c.png)
![\begin{align}
\left]a,b\right[ &= \{x\,|\, a< x < b\}, \\
\left[a,b\right[ &= \{x\,|\, a\le x < b\}, \\
\left]a,b\right] &= \{x\,|\, a< x \le b\}, \\{}
[a,b] &= \{ x \,| \,a \le x \le b \}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c7109a90aea2b412c275c383a4dbb181.png)